Рассмотрю прямоугольный тетраэдр, у которого В вершин, Р ребер и Г граней. По теореме Эйлера для него должно выполняться равенство:

В - Р + Г = 2

У прямоугольного тетраэдра 4 грани, 4 вершины и 6 рёбер.
Подставляем данные в формулу Эйлера:

4 - 6 + 4 = 2

Из этого следует, что для прямоугольного тетраэдра справедлива теорема Эйлера.

 

Дано: прямоугольный тетраэдр, где В - вершины, Р - ребра, Г - грани.
Доказать: В - Р + Г = 2
Доказательство:
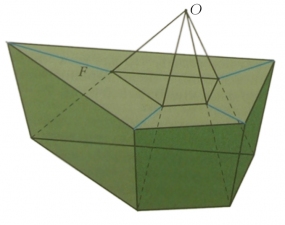
Возьму снаружи многогранника точку О вблизи от какой-либо грани F и спроектирую остальные грани на F из центра О (рис. 17).

Рис. 17

Их проекции образуют разбиение грани F на многоугольники. Подсчитаю двумя способами сумму σ углов всех полученных многоугольников и самой грани F. Сумма углов n-угольника равна π(n - 2). Сложу эти числа для всех граней (включая и грань F). Сумма членов вида πn равна общему числу сторон всех граней, т. е. 2P - ведь каждое из Р рёбер принадлежит двум граням. А так как всего у меня Г слагаемых, σ=π(2Р-2Г). Теперь найду сумму углов при каждой вершине разбиения и сложу эти суммы. Если вершина лежит внутри грани F, то сумма углов вокруг неё равна 2π. Таких вершин В-k, где k - число вершин самой грани F, а значит, их вклад в σ равен 2π(B-k). Углы при вершинах F считаются в сумме σ дважды (как углы F и как углы многоугольников разбиения); их вклад равен 2π(k-2). Таким образом, σ=2π(B-k)+2π(k-2)=2π(B-2). Приравнивая два результата и сокращая на 2π, получу требуемое равенство Р - Г = В - 2.
Величина В - Р + Г, называемая эйлеровой характеристикой, будет равна 2 для всех многогранников, «устроенных, как сфера», - они, образно говоря, превратятся в шарик, если их сделать из резины и надуть.