УГЛЫ В ПРЯМОУГОЛЬНОМ ТЕТРАЭДРЕ
Двугранные углы, каждый из которых является пересечением двух из трех полупространств, образующих тетраэдр, называются двугранными углами этого тетраэдра.

На рисунке 3 плоские углы при вершине B - прямые.

Рис. 3

Величины α, β, γ, δ, ε, φ плоских углов BCD, CDB, DAB, ADB, BAC, BCA соответственно находятся в открытом промежутке от 0˚ до 180˚, так как каждый из них является пересечением двух полуплоскостей.

Неравенства для углов тетраэдра

Сумма плоских углов тетраэдра.
Эта сумма, очевидно, непостоянна. Однако она меньше 270˚:
Дано: прямоугольный тетраэдр DABC

Доказать:

(1)

Доказательство: На рисунке 4 при вершине B сумма углов равна 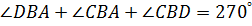, т.к. 90˚+90˚+90˚=270˚. При других вершинах это значение будет меньше.

(2)

Теперь рассмотрю случай, когда ∠DCA=90˚. А углы ∠BCA и ∠BCD острые, так как △BCA и △BCD прямоугольные. Следовательно, равенство 2 справедливо.

Рис. 4