Простейшим многогранником является тетраэдр - четырехгранник. Он обладает многими замечательными свойствами, совокупность которых принято называть геометрией тетраэдра. Рассмотрю сейчас некоторые из них.
Отрезки, каждый из которых соединяет середины противоположных (скрещивающихся) ребер тетраэдра, называются его бимедианами (средними линиями).
Теорема. Бимедианы тетраэдра пересекаются в одной точке, которая делит пополам каждую из них.
Дано: прямоугольный тетраэдр ABCD, MN, EF и PQ - бимедианы
Доказать: MN∩EF∩PQ=G, 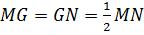
Доказательство 1. Пусть на рисунке 5 при вершине D 3 плоских
угла - прямые; MN, EF и PQ - бимедианы прямоугольного тетраэдра ABCD, соответствующие парам ребер AB и CD, AC и BD, BC и AD (рис. 5). Так как отрезки ME и FN параллельны BC и равны половине BC, то четырехугольник EMFN - параллелограмм. Точка G пересечения его диагоналей MN и EF делит их пополам. Из параллелограмма EPFQ следует, что середины бимедиан EF и PQ совпадают с точкой G.
Доказательство 2. Для произвольной точки O векторы
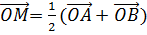
и
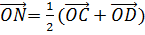
Поэтому 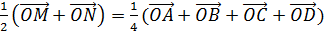
Следовательно, вектор 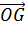 середины G отрезка
середины G отрезка 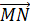 имеет выражение
имеет выражение
в которое векторы вершин тетраэдра входят равноправно (симметрично). Это значит, что векторы середин отрезков EF и PQ также равны 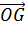 , т. е. середины бимедиан MN, EF и PQ совпадают. Точка G пересечения бимедиан тетраэдра называется его центроидом. Для произвольной точки O вектор
, т. е. середины бимедиан MN, EF и PQ совпадают. Точка G пересечения бимедиан тетраэдра называется его центроидом. Для произвольной точки O вектор 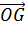 центроида тетраэдра имеет выражение (6).
центроида тетраэдра имеет выражение (6).

