Дано: прямоугольный тетраэдр DABC
Доказать: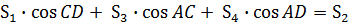 
Доказательство: Обозначу площади граней BCD, ACD, ABC и ABD соответственно S1, S2, S3 и S4 (рис. 11). Плоскость ACD наклонена к плоскости ABC под углом φ1; ABD, BCD под углом равным 90˚ =>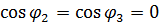 
Основание высоты из вершины B прямоугольного тетраэдра DABC попадает внутрь грани ACD и, используя формулу ортогональной, проекции получаю:
Подставляя (11) (12) (13), получаю:
Следствие 1: Пусть B - ортогональная проекция вершины D тетраэдра DABC на плоскость грани ABC.
Получаю, по теореме о площади ортогональной проекции:
Но это справедливо только для вершин A, D, C.
Следствие 2: Площадь любой грани тетраэдра меньше суммы площадей трех остальных его граней:
Введение
Определение
Применение
