Из выведенных ранее формул объема тетраэдра в качестве следствий получаются соотношения, очень похожие на теоремы синусов для треугольника и триэдра.

По формуле Штаудта

Рис. 16

Разделю эти равенства почленно на произведение abca₁b₁c₁:

 

Синусы Штаудта трехгранных углов тетраэдра пропорциональны произведениям длин трех ребер граней, противолежащих этим углам (первая теорема синусов).
Пользуясь формулой (18), аналогичным путем получаю:

 

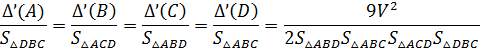
Синусы второго рода трехгранных углов тетраэдра пропорциональны площадям противолежащих им граней (вторая теорема синусов). Далее, перемножим два равенства из (17):

 

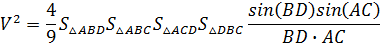
Из этого соотношения и двух ему аналогичных следует:

 

 

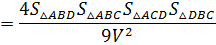
Произведения длин противоположных ребер тетраэдра пропорциональны произведениям синусов соответствующих двугранных углов (третья теорема синусов).