Теорема. Объём прямоугольного тетраэдра равен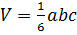 
Дано: ABCD - прямоугольный тетраэдр
Доказать: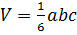
Доказательство: ABCD - прямоугольный тетраэдр, AB=a, BC=b, BD=c (рис. 12).
Я знаю, что объем пирамиды находится по формуле:
где Sосн - площадь основания, h - высота.
Выберу основанием ∆ABC, тогда a будет высотой прямоугольного тетраэдра. Площадь основания примет вид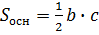 
Подставляю в формулу объема пирамиды мои значения и получаю, что:
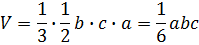
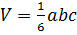, что и требовалось доказать.
Теорема. Объём прямоугольного тетраэдра равен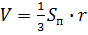 
Дано: Прямоугольный тетраэдр ABCD, T - центр вписанной сферы, TK = r радиус вписанной сферы, Sп - площадь полной поверхности прямоугольного тетраэдра.
Доказать: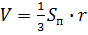
Доказательство:
Объем прямоугольного тетраэдра ABCD складывается из объемов тетраэдров TADB, TBCD, TABC, TADC (рис. 13).
В данном случае высотой является радиус вписанной окружности, т.е. r.
Используя формулу 16, получаю:
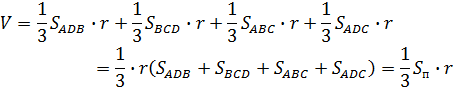
Ч.т.д.
ПЕРВАЯ ФОРМУЛА ШТАУДТА. За исходные формулы объема тетраэдра возьму две известные формулы:
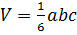и 
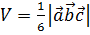
где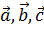 
- векторы трех ребер тетраэдра с общим началом в его вершине. Выведу другие формулы объема тетраэдра.
Пусть ребро DB - высота прямоугольного тетраэдра ABCD, AH - высота его грани ACD (рис. 14).
Тогда
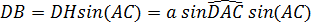
. Поэтому
.
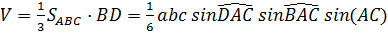
Произведение
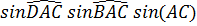
есть синус Штаудта Δ(A) трехгранного угла A(BCD).
Итак,
.
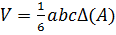
Эта формула известна под именем немецкого геометра Карла Штаудта (1798–1867), профессора Эрлангенского университета. Без использования обозначений ее можно высказать так: объем тетраэдра равен шестой части произведения длин трех ребер с общей вершиной и синуса Штаудта его триэдра с этой вершиной
Введение
Определение
Применение
