| Неравенства для прямоугольного тетраэдра |
|
|
| |
В таком тетраэдре OABC ребра OA, OB, OC попарно перпендикулярны. Приму следующие обозначения: OA=a, OB=b, OC=c, S1, S2, S3, S - площади граней OBC, OCA, OAB, ABC соответственно, h - высота тетраэдра, проведенная к грани ABC, R и r - радиусы описанной и вписанной сфер, V - объем.
На основании неравенства (22) 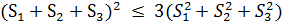 . Поскольку . Поскольку 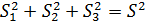 , то , то
Левое из этих неравенств совпадает с неравенством 15б) для тетраэдра общего вида. Так как 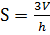 , 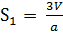 ,  , 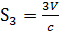 , то неравенство (25) равносильно такому:
Принимая во внимание, что , то неравенство (25) равносильно такому:
Принимая во внимание, что 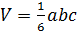 , на основании неравенства Коши получаю: , на основании неравенства Коши получаю:
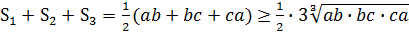
Таким образом,
Разделю равенство 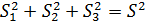 на на 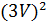 . В результате буду иметь соотношение: . В результате буду иметь соотношение:
Используя неравенство Коши, получаю:
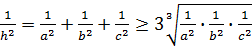
откуда
и поэтому
Дострою тетраэдр OABC до прямоугольного параллелепипеда. Учитывая, что радиус R описанной сферы равен половине диагонали этого параллелепипеда, а медиана OM тетраэдра - трети диагонали. Так как высота h не больше медианы OM, то 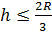 , те есть , те есть
Из формулы 24 при 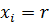 получу: получу:
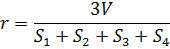
Откуда 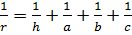 , то , то 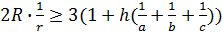 .На основании (26) .На основании (26) 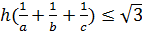 . Следовательно, . Следовательно,
Во всех полученных неравенствах знак равенства имеет место лишь при a=b=c. |
|
|

