Треугольник называ­ется пифагоровым, если у него один угол прямой, а отношение любых других сторон рационально (тогда, применяя подобие, можно из него по­лучить прямоугольный треугольник с целыми длинами сторон). По анало­гии с этим будем называть тетраэдр пифагоровым, если его плоские углы при одной из вершин прямые, а от­ношение любых двух ребер рацио­нально (из него с помощью подобия можно получить тетраэдр с прямы­ми плоскими углами при одной из вершин и целыми длинами ребер).

Сейчас я выведу «уравнение пифагоровых тетраэдров», то есть такое уравнение с тремя неизвестными ξ, η, ς, что любой пифагоров тетраэдр дает рациональное решение этого уравнения, и наоборот, любое рациональное решение уравнения дает пифагоров тетраэдр. А затем, пользуясь этим уравнением, найду конкретные примеры пифагоровых тетраэдров.

Пифагоровы треугольники

Сначала дам способ описания всех пифагоровых треугольников. На рисунке 21 треугольник ОАВ - прямоугольный; длины его катетов обозначены через a и b, а длина гипотенузы - через р. Число

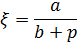
(33)

Рис. 21

условлюсь называть параметром прямоугольного треугольника ОАВ (или, точнее, параметром «относительно катета а»). Используя соотношение р²=а²+Ь², имею

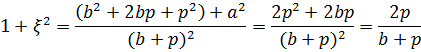
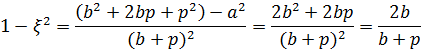
Из этих равенств непосредственно получаю формулы, выражающие отношения сторон прямоугольного треугольника через его параметр:

,

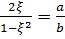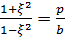
(34)

Из формул (33) (34) непосредственно вытекает следующее утверждение: для того чтобы прямоугольный треугольник был пифагоровым, необходимо и достаточно, чтобы число ξ было рациональным. В самом деле, если треугольник пифагоров, то из (33) следует, что ξ рационально. Обратно, если ξ рационально, то согласно (34) отношения сторон рациональны, то есть треугольник пифагоров.

Уравнение пифагоровых тетраэдров

Пусть теперь ОАВС - тетраэдр, у которого плоские углы при вершине О прямые. Длины ребер, исходящих из вершины О, обозначу через а, Ь, с, а длины трех других ребер - через p, q, r (рис. 22). Рассмотрю параметры трех прямоугольных треугольников ОАВ, ОВС, ОСА:

, , (35)

Рис. 22

Тогда по формулам (34) можно выразить отношения сторон этих прямоугольных треугольников через их параметры:

, , ;

(36)