| Свойства центроида тетраэдра, теорема Лейбница |
|
|
| |
Центроид прямоугольного тетраэдра является центром равных масс, помещённых в его вершины.
1. Для того чтобы точка G была центроидом прямоугольного тетраэдра ABCD, необходимо и достаточно, чтобы 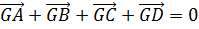
Дано: прямоугольный тетраэдр ABCD
Доказательство: Если G — центроид прямоугольного тетраэдра ABCD, то имеет место равенство (6) для произвольной точки O (рис. 7).
Когда точка O совпадает с G, то 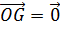 и (6) принимает вид (7). Обратно, пусть для некоторой точки G имеет место равенство (7), из которого и (6) принимает вид (7). Обратно, пусть для некоторой точки G имеет место равенство (7), из которого 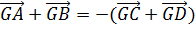 , или , или 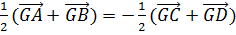 , или , или 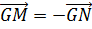 , где M и N — середины ребер AB и CD. Следовательно, точка G является серединой бимедианы MN, т. е. центроидом тетраэдра. , где M и N — середины ребер AB и CD. Следовательно, точка G является серединой бимедианы MN, т. е. центроидом тетраэдра.
2. Другое свойство центроида прямоугольного тетраэдра связано с объемами: тетраэдры GBCD, GCDA, GDAB, GABC равновелики. Действительно, отношение высот AH и GH1 тетраэдров ABCD и GBCD равно отношению 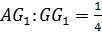 (рис. 7). Эти тетраэдры имеют общее основание BCD. Значит, (рис. 7). Эти тетраэдры имеют общее основание BCD. Значит, 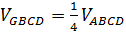 . Объем каждого из четырех указанных тетраэдров равен четверти объема данного тетраэдра. В силу этого свойства центроид прямоугольного тетраэдра называют еще центром тяжести этого тетраэдра. . Объем каждого из четырех указанных тетраэдров равен четверти объема данного тетраэдра. В силу этого свойства центроид прямоугольного тетраэдра называют еще центром тяжести этого тетраэдра.
Теорема Лейбница. Сумма квадратов расстояний от произвольной точки P до вершин прямоугольного тетраэдра A1A2A3A4 равна сумме квадратов расстояний от его центроида G до вершин, сложенной с учетверенным квадратом расстояния от точки P до центроида G:
Действительно, 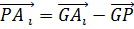 , откуда , откуда 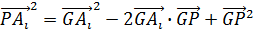 и поэтому и поэтому
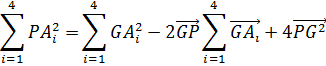
Так как 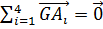 , то равенство (8) доказано. Из теоремы Лейбница следует экстремальное свойство центроида прямоугольного тетраэдра: сумма квадратов расстояний от точки до вершин тетраэдра минимальна для его центроида. Оно является характеристическим свойством центроида прямоугольного тетраэдра. , то равенство (8) доказано. Из теоремы Лейбница следует экстремальное свойство центроида прямоугольного тетраэдра: сумма квадратов расстояний от точки до вершин тетраэдра минимальна для его центроида. Оно является характеристическим свойством центроида прямоугольного тетраэдра.
|
|
|

