ОПРЕДЕЛЕНИЕ ПРЯМОУГОЛЬНОГО ТЕТРАЭДРА
Многогранник - геометрическое тело, граница (поверхность) которого есть объединение конечного числа многоугольников.

Тетра́эдр - многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Любая грань тетраэдра может быть принята за его основание.

Тетраэдр называется прямоугольным, если три плоских угла при одной вершине прямые.

Пусть Q - плоский многоугольник в плоскости α и S - точка, не принадлежащая плоскости α. Соединю каждую точку М многоугольника Q с точкой S отрезком MS. Отрезки MS заполняют некоторый многогранник. Этот многогранник называется пирамидой (рис. 1).

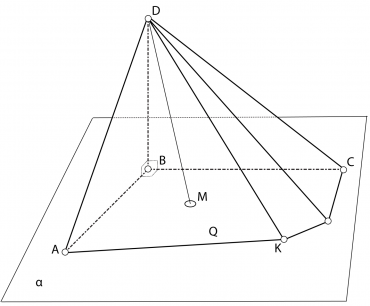Рис. 1

Треугольная пирамида называется тетраэдром. Многоугольник Q называется основанием пирамиды, а точка S - вершиной пирамиды. Высотой пирамиды называется отрезок перпендикуляра, проведенного через вершину к плоскости ее основания; концами этого отрезка являются вершина пирамиды и основание перпендикуляра; на рисунке 1 DB - высота пирамиды. (Высотой пирамиды называют и длину этого отрезка.) Пусть A, B, C, ... K - вершины многоугольника Q, лежащего в основании пирамиды. Тогда треугольники ADB, BDC, ... , KDA называются боковыми гранями пирамиды, а отрезки AD, BD, CD, ... , KD боковыми ребрами.
Часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию, называется усеченной пирамидой (рис. 2).

Параллельные грани ABC и А₁В₁С₁ на­зываются основаниями, а отрезок перпендикуляра ОО₁ 

Рис. 2

опущенного из какой-нибудь точки О₁ верхнего основания на нижнее основание, - высотой усеченной пирамиды. ОО₁  BB₁, BB₁ - высота усеченного прямоугольного тетраэдра.