| Теорема о площади ортогональной проекции |
|
|
| |
Рассмотрю вопрос о формуле проекций граней прямоугольного тетраэдра. Предварительно рассмотрю ортогональное проектирование отрезка, лежащего в плоскости α, выделив два случая расположения этого отрезка относительно прямой l=α∩π.
Случай 1. AB∥l (рис. 8). Отрезок A1B1, являющийся ортогональной проекцией отрезка AB, равен и параллелен отрезку АВ.
Случай 2. CD⊥l (рис. 8). По теореме о трех перпендикулярах прямая C1D1, являющаяся ортогональной проекцией прямой CD, также перпендикулярна прямой l. Следовательно, ∠CEC1 — угол между плоскостью α и плоскостью проекций π, т. е. 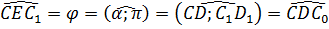 , где C0D=C1D1. Поэтому |C1D1|=|CD|∙cosφ , где C0D=C1D1. Поэтому |C1D1|=|CD|∙cosφ
Теперь рассмотрю вопрос об ортогональном проектировании треугольника.
Площадь ортогональной проекции треугольника на плоскость равна площади проектируемого треугольника, умноженной на косинус угла между плоскостью треугольника и плоскостью проекций.
Доказательство. Площадь проекции треугольника.
а) Пусть одна из сторон, например АС, проектируемого треугольника ABC параллельна прямой l=α∩π (рис. 9) или лежит на ней.
Тогда его высота ВН перпендикулярна прямой l, а площадь равна 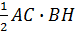 , т. е. , т. е.
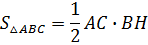
На основании выше рассмотренных свойств ортогональной проекции отрезка имею:
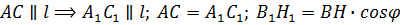
По теореме о трех перпендикулярах прямая B1H1 — ортогональная проекция прямой ВН — перпендикулярна прямой l, следовательно, отрезок В1Н1 — высота треугольника A1B1C1. Поэтому 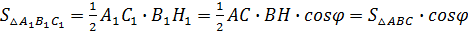 . Таким образом, . Таким образом, 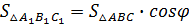 . .
б) Ни одна из сторон проектируемого треугольника ABC не параллельна прямой l (рис. 10). Проведу через каждую вершину треугольника прямую, параллельную прямой l. Одна из этих прямых лежит между двумя другими (на рисунке — это прямая m), и, следовательно, разбивает треугольник ABC на треугольники ABD и ACD с высотами соответственно ВН и СЕ, проведенными к их общей стороне AD (или ее продолжению), которая параллельна l. Прямая m1 — ортогональная проекция прямой m — также разбивает треугольник А1В1С1 — ортогональную проекцию треугольника ABC — на треугольники A1B1D1 и A1C1D1, где 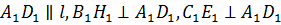 . Принимая во внимание (9) и (10), получаю . Принимая во внимание (9) и (10), получаю
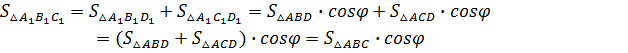
Итак, для произвольно расположенного в плоскости α треугольника ABC выполняется 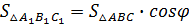 |
|
|

