Так как равенства (23) не зависят от точки O, то в качестве такой точки можно взять точку A₄:

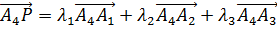
Умножу это равенство скалярно на вектор :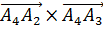

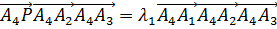
откуда

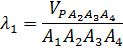
где тетраэдры A₁A₂A₃A₄ и PA₂A₃A₄ считаются ориентированными соответственно указанным тройкам векторов. Аналогично получу:

, ,

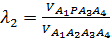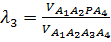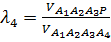
Итак, барицентрические координаты λ_i точки P равны отношениям объемов двух ориентированных тетраэдров: объема тетраэдра, полученного заменой соответствующей вершины базисного тетраэдра A₁A₂A₃A₄ точкой P, к объёму тетраэдра A₁A₂A₃A₄.
Пусть x_i - ориентированные расстояния точки P до плоскостей граней прямоугольного тетраэдра A₁A₂A₃A₄, причем за положительное направление принято направление соответствующей высоты h_i этого тетраэдра от вершины к противоположной грани. Тогда отношения объемов указанных тетраэдров равны 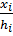(i=1,2,3,4). Следовательно, 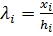и

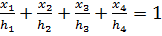
Умножив последнее равенство на 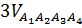, получу:

(24)

Числа x_i называются нормальными координатами точки P относительно данного тетраэдра. При этом x_i=λ_ih_i.